Introduction
Unlike the gates such as the Pauli X or CNOT gate it can be difficult for beginners to understand what the Z-gate actually does and why it is used.
In this tutorial we will explore the Z-gate including what it does and how to implement it in Python and Qiskit.
WHAT IS THE Z-GATE?
The Z-gate is a unitary gate that acts on only one qubit. Specifically it maps 1 to -1 and leaves 0 unchanged. It does this by rotating around the Z axis of the qubit by π radians (180 degrees). By doing this it flips the phase of the qubit.
But what actually happens when we use this gate?
Unless we are in a superposition of states not much since the phase doesn’t matter when the qubit is in the computational basis (0 or 1).
Example:
-
If our qubit is initialised to 0 and we apply a Z-gate and measure we will get a 0.
-
If our qubit is initialised to 1 and we apply a Z-gate then we will get -1 (Note: this is just 1 but with the phase changed so when measured it will be 1)
PHASE FLIP CIRCUIT
So applying the Z-gate to an initialised qubit will leave the qubits computational state unchanged when measured.
However if we apply a hadamard gate first then a Z-gate and then a hadamard gate it will flip the phase of the qubit.

Phase Flip Circuit
Example:
-
If we initialise our qubit to 0 and use the phase flip circuit above then we will get 1 when measured
-
If we initialise our qubit to 1 and use the phase flip circuit we will get a 0 instead.
HOW DOES THIS WORK?
When we apply a hadamard gate to a qubit it puts it in to a superposition of states such that when measured it could be 0 or 1 with equal probability.
However if we apply a hadamard gate again and then measure then it returns back from a superposition to its initialised state.
Hence HH = I where I just means identity.
Example: if we have our qubit set to 0 and apply a hadamard gate it will go in to a superposition of states. If we apply the hadamard gate again then it flips it back to 0 when measured.
However if we apply a Z-gate between those two hadamard gates it flips the phase 180 degrees and as such when measured it isn’t back in to its initialised state but the opposite.
This is extremely useful as it means even though our qubit is in superposition we can conserve information within the qubit.
As such it is used in many important quantum algorithms such as in Superdense coding where we encode 2 classical bits in 1 qubit.
Superdense coding tutorial: https://quantumcomputinguk.org/tutorials/superdense
Code
Note: For this tutorial you will need an API token which you can get by registering here: https://quantum-computing.ibm.com/
Once you have it copy and paste in to the IBMQ.enable_account(‘Enter API token here’) function in the code.
print('\nZ gate tutorial')
print('-----------------')
from qiskit import QuantumRegister
from qiskit import QuantumRegister, ClassicalRegister
from qiskit import QuantumCircuit, execute,IBMQ
IBMQ.enable_account('Enter API token here')
provider = IBMQ.get_provider(hub='ibm-q')
backend = provider.get_backend('ibmq_qasm_simulator')
q = QuantumRegister(1,'q')
c = ClassicalRegister(1,'c')
##### Z gate when qubit is 0 #######################################
circuit = QuantumCircuit(q,c)
circuit.z(q[0]) # Applying z gate
circuit.measure(q,c)# Measuring qubit
job = execute(circuit, backend, shots=100)
print('\nExecuting...\n')
result = job.result()
counts = result.get_counts(circuit)
print('\n Z when qubit is 0\n')
print('RESULT: ',counts,'\n')
#####################################################
##### Z gate when qubit is 1 #######################################
circuit = QuantumCircuit(q,c)
circuit.x(q[0])# Used to initialise qubit to 1
circuit.z(q[0])
circuit.measure(q,c)
job = execute(circuit, backend, shots=100)
print('\nExecuting...\n')
result = job.result()
counts = result.get_counts(circuit)
print('\n Z when qubit is 1\n')
print('RESULT: ',counts,'\n')
#####################################################
##### H H #########################################
circuit = QuantumCircuit(q,c)
circuit.h(q[0])
circuit.h(q[0])
circuit.measure(q,c)
job = execute(circuit, backend, shots=100)
print('\nExecuting...\n')
result = job.result()
counts = result.get_counts(circuit)
print('\n H H \n')
print('RESULT: ',counts,'\n')
#####################################################
##### H Z H when qubit is 0 ########################
circuit = QuantumCircuit(q,c)
circuit.h(q[0])
circuit.z(q[0])
circuit.h(q[0])
circuit.measure(q,c)
job = execute(circuit, backend, shots=100)
print('\nExecuting...\n')
result = job.result()
counts = result.get_counts(circuit)
print('\n H Z H when qubit is 0 \n')
print('RESULT: ',counts,'\n')
####################################################
##### H Z H when qubit is 1 ########################
circuit = QuantumCircuit(q,c)
circuit.x(q[0]) # Used to initialise qubit to 1
circuit.h(q[0])
circuit.z(q[0])
circuit.h(q[0])
circuit.measure(q,c)
job = execute(circuit, backend, shots=100)
print('\nExecuting...\n')
result = job.result()
counts = result.get_counts(circuit)
print('\n H Z H when qubit is 1 \n')
print('RESULT: ',counts,'\n')
####################################################
print('Press any key to close')
input()Output
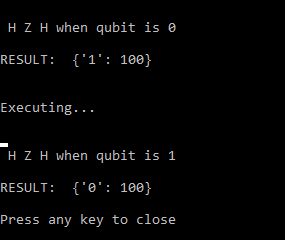
Output showing results from the phase flip circuit when the qubit is initialised to both 0 and 1