A team of researchers from California Institute of Technology recently introduced a new method that can be used to predict multiple properties of complex quantum systems from a limited number of measurements, according to Phys.org. The method, outlined in a paper published in Nature Physics, has been found to be highly efficient and could open up new possibilities for studying the ways in which machines process quantum information.
“During my undergraduate, my research centered on statistical machine learning and deep learning,” Hsin-Yuan Huang, one of the researchers who carried out the study, told Phys.org. “A central basis for the current machine-learning era is the ability to use highly parallelized hardware, such as graphical processing units (GPU) or tensor processing units (TPU). It is natural to wonder how an even more powerful learning machine capable of harnessing quantum-mechanical processes could emerge in the far future. This was my aspiration when I started my Ph.D. at Caltech.”
The first step toward the development of more advanced machines based on quantum-mechanical processes is to gain a better understanding of how current technologies process and manipulate quantum systems and quantum information. The standard method for doing this, known as quantum state tomography, works by learning the entire description of a quantum system. However, this requires an exponential number of measurements, as well as considerable computational memory and time.
As a result, when using quantum state tomography, machines are currently unable to support quantum systems with over tens of qubits. In recent years, researchers have proposed a number of techniques based on artificial neural networks that could significantly enhance the quantum information processing of machines. Unfortunately, however, these techniques do not generalize well across all cases, and the specific requirements that allow them to work are still unclear.
“To build a rigorous foundation for how machines can perceive quantum systems, we combined my previous knowledge about statistical learning theory with Richard Kueng and John Preskill’s expertise on a beautiful mathematical theory known as unitary t-design,” Huang said. “Statistical learning theory is the theory that underlies how the machine could learn an approximate model about how the world behaves, while unitary t-design is a mathematical theory that underlies how quantum information scrambles, which is central to understand quantum many-body chaos, in particular, quantum black holes.”
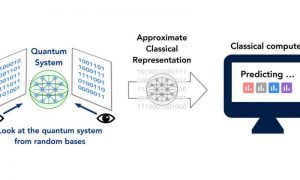
By combining statistical learning and unitary t-design theory, the researchers were able to devise a rigorous and efficient procedure that allows classical machines to produce approximate classical descriptions of quantum many-body systems. These descriptions can be used to predict several properties of the quantum systems that are being studied by performing a minimal number of quantum measurements.
“To construct an approximate classical description of the quantum state, we perform a randomized measurement procedure given as follows,” Huang said. “We sample a few random quantum evolutions that would be applied to the unknown quantum many-body system. These random quantum evolutions are typically chaotic and would scramble the quantum information stored in the quantum system.”
The random quantum evolutions sampled by the researchers ultimately enable the use of the mathematical theory of unitary t-design to study such chaotic quantum systems as quantum black holes. In addition, Huang and his colleagues examined a number of randomly scrambled quantum systems using a measurement tool that elicits a wave function collapse, a process that turns a quantum system into a classical system. Finally, they combined the random quantum evolutions with the classical system representations derived from their measurements, producing an approximate classical description of the quantum system of interest.
“Intuitively, one could think of this procedure as follows,” Huang explained. “We have an exponentially high-dimensional object, the quantum many-body system, that is very hard to grasp by a classical machine. We perform several random projections of this extremely high-dimension object to a much lower dimensional space through the use of random/chaotic quantum evolution. The set of random projections provides a rough picture of how this exponentially high dimensional object looks, and the classical representation allows us to predict various properties of the quantum many-body system.”
Huang and his colleagues proved that by combining statistical learning constructs and the theory of quantum information scrambling, they could accurately predict M properties of a quantum system based solely on log(M) measurements. In other words, their method can predict an exponential number of properties simply by repeatedly measuring specific aspects of a quantum system for a specific number of times.
“The traditional understanding is that when we want to measure M properties, we have to measure the quantum system M times,” Huang said. “This is because after we measure one property of the quantum system, the quantum system would collapse and become classical. After the quantum system has turned classical, we cannot measure other properties with the resulting classical system. Our approach avoids this by performing randomly generated measurements and infer the desired property by combining these measurement data.”
The study partly explains the excellent performance achieved by recently developed machine learning (ML) techniques in predicting properties of quantum systems. In addition, its unique design makes the method they developed significantly faster than existing ML techniques, while also allowing it to predict properties of quantum many-body systems with a greater accuracy.
“Our study rigorously shows that there is much more information hidden in the data obtained from quantum measurements than we originally expected,” Huang said. “By suitably combining these data, we can infer this hidden information and gain significantly more knowledge about the quantum system. This implies the importance of data science techniques for the development of quantum technology.”
The results of tests the team conducted suggest that to leverage the power of machine learning, it is first necessary to attain a good understanding of intrinsic quantum physics mechanisms. Huang and his colleagues showed that although directly applying standard machine-learning techniques can lead to satisfactory results, organically combining the mathematics behind machine learning and quantum physics results in far better quantum information processing performance.
“Given a rigorous ground for perceiving quantum systems with classical machines, my personal plan is to now take the next step toward creating a learning machine capable of manipulating and harnessing quantum-mechanical processes,” Huang said. “In particular, we want to provide a solid understanding of how machines could learn to solve quantum many-body problems, such as classifying quantum phases of matter or finding quantum many-body ground states.”
This new method for constructing classical representations of quantum systems could open up new possibilities for the use of machine learning to solve challenging problems involving quantum many-body systems. To tackle these problems more efficiently, however, machines would also need to be able to simulate a number of complex computations, which would require a further synthesis between the mathematics underlying machine learning and quantum physics. In their next studies, Huang and his colleagues plan to explore new techniques that could enable this synthesis.
“At the same time, we are also working on refining and developing new tools for inferring hidden information from the data collected by quantum experimentalists,” Huang said. “The physical limitation in the actual systems provides interesting challenges for developing more advanced techniques. This would further allow experimentalists to see what they originally could not and help advance the current state of quantum technology.”