Let’s Recap!
We have gone through quite a journey with regards to entanglement so far. Here a list of the previous posts in this series:
- The Classical Interpretation of Controlled Operations
- Representing Entanglement with Graphs and Hypergraphs
- Quantum Programming: Building the Bell State Graph
- Destroying Entanglement in a Bell State
But why is this relevant? what are the advantages of going through the trouble of using such a model instead of the standard wave function state vector concept?
Simulating quantum algorithms efficiently
Simulating quantum computation is a pretty active area of research. There is a really healthy balance between research efforts towards demonstrating quantum advantage versus improving classical simulation. There’s a lot of technological benefits to discover from both approaches.
There are currently some interesting techniques like Tensor Networks that allow you to simulate a certain specific type of quantum circuits efficiently by compressing data in specific structures like for example, tensors. This is useful because the main issue with “raw” simulation is that a state vector grows exponentially with the number of qubits and at some point, we do not have enough classical power to even store the data.
The Hypergraph model that we have been working on in this series seems like a good candidate for a more efficient simulation. Let’s take a look at it.
Analyzing the Cost of Evolution
In a previous post, we briefly discussed a way to calculate the wave function given a hypergraph but if we take this calculation out of our analysis (as it would obviously run against the same scaleability issues with raw state vector simulation) we are left with the cost analysis of how our model evolves and grows in time. Not being able to store the full wave function is not really an issue because it is actually a bit closer to how we will interact with real QPUs in real-world scenarios.
If we follow closely the example we outlined here we can see 2 things:
- Single qubit operations do not “add” information to the model. When we apply a single qubit operation we change the state of 1 or more nodes.
- Controlled operations seem to add information but it is not clear how this scales with the number of qubits as we have only been playing with 2-qubit examples.
The Toffoli Gate Example
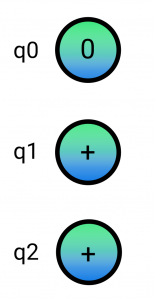
In order to investigate controlled operations further let’s play with this small example. Let’s imagine we start off with a system in the following 3 qubit state (we ignore amplitudes for simplicity and assume an equal superposition):
a|000> +b|001> + c|010> + d|011>
How would a CCX Gate transform the state with the controlled qubits being the middle (q1) and the right-most one (q2)? We can easily build the corresponding hypergraph by just assuming the system is fully entangled and each component is in a separate hyperedge. This leads to the following hypergraph:
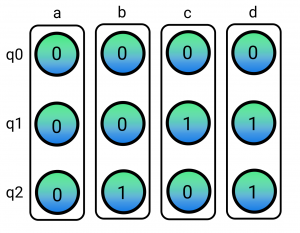
We can immediately see that all the nodes of qubit 0 are in the same state and so this an indication the hypergraph could be simplified as we did in the past post with a smaller example. After simplifying (left as an exercise for the curious reader) we end up with a very simple hypergraph (note that none of the nodes belongs to any hyperedge, hence the system is not entangled):
In order to implement the CCX Gate, we can follow a similar logic to what we designed originally the CX gate to do: Split nodes and create hyperedges. But how do we split them? We now have 2 nodes that are being controlled so we could think of splitting them separately and applying the target gate (X Gate) within the corresponding edges. After splitting q1 we run into the first problems.
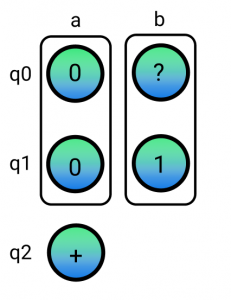
We can’t tell whether the q0 node in the hyperedge b will be a 0 or a 1 because we do not have information about q2 within the b edge. Another issue is that if we now split q2 we do not really know what to do with the resulting nodes. Do we put the 0 and 1 to each edge? which edges do we pick for each node?
If we think about it carefully there is no reason to think about q1 and q2 separately as it is the combined values of both that define the application of the target gate. Classically speaking we would need to at least consider 4 possible pairs of values: 00,01,10 and 11 so let’s try splitting the system into 4 hyperedges in one step and then apply X to q0 within the edge where q1 and q2 are 1 (edge d):
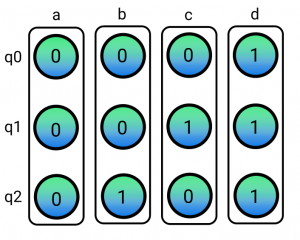
Now, this makes more sense! We can at least specify the value of each q0 node without any problem and if we calculate the state vector following the steps we described in this older post we obtain the correct state vector
a|000> + b|001> + c|010> + d|111>
What have we learned?
There is both good and bad news out of this example. On one side we just saw that we had to create 4 hyperedges when controlling on 2 qubits. With one qubit, we had to create 2 edges and so this seems to indicate that for circuits with a lot of entangled qubits our model sadly grows exponentially. Sometimes we can compress our state a bit more by simplifying the hypergraph like this:
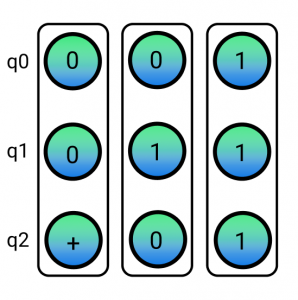
But the worst-case scenario is still a present factor. On the other side, the good news is that for circuits that exhibit less entanglement it is a good tool to simulate bigger systems.
Another interesting observation is that the model puts entanglement and the distribution of information at the forefront. This seems like it could be useful as an aid for the design of algorithms where entanglement between registers is key (Shor’s algorithm is an example we will soon explore).
What’s next?
In the next post, we will explore the reason behind why 4 hyperedges were enough to implement the CCX operation. You might ask yourself where are all the in-between states one can have in a quantum system? Why is 4 enough? We’ll discover that soon.